博客
关于我
强烈建议你试试无所不能的chatGPT，快点击我
纪中21日T3 2118. 【2016-12-30普及组模拟】最大公约数
阅读量：5272 次
发布时间：2019-06-14

本文共 6092 字，大约阅读时间需要 20 分钟。

纪中21日T3 2118. 最大公约数

(File IO): input:gcd.in output:gcd.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制  

题目描述

给出两个正整数A，B，求它们的最大公约数。

输入

第一行一个正整数A。

第二行一个正整数B。

输出

在第一行输出一个整数，表示A，B的最大公约数。

样例输入

18 24 

样例输出

6 

数据范围限制

在40%的数据中，1 ≤ A，B ≤ 10^6

在60%的数据中，1 ≤ A，B ≤ 10^18
在80%的数据中，1 ≤ A，B ≤ 10^100
在100%的数据中，1 ≤ A，B ≤ 10^1000

Solution

Algorithm1

正常的gcd（a，b）=gcd（b，a%b）；

开unsigned long long可得六十分（应该不会超时）

Code1

#include
     
      #include
      
       #include
       
        #include
        
         #include
         
          #include
          #include
           
            #include
            
             #include
             
              #define IL inlineusing namespace std;unsigned long long gcd(unsigned long long a,unsigned long long b){ return b==0?a:gcd(b,a%b);}unsigned long long a,b;int main(){ cin>>a>>b; cout<

Attention1

函数也要开ULL（缩写）

别把“%”写成“-”，否则在相减前要先使得a>b

而且那样就变成更相减损法了

Algorithm2

gcd二进制法

先看看a，b是不是2的倍数

如果都是，gcd（a，b）=2*gcd（a/2，b/2）；

如果a是，gcd（a，b）=gcd（a/2，b）；

如果b是，gcd（a，b）=gcd（a，b/2）；

如果都不是，gcd（a，b）=gcd（b，a%b）

最后一条=gcd（b，a-b）也可以

（为后面的高精度做铺垫）

Code2

1 #include
      
        2 #include
       
         3 #include
        
          4 #include
         
           5 #include
          
            6 #include
           
             7 #include
             8 #include
             
               9 #include
              
               10 #include
               
                11 #define IL inline12 using namespace std;13 IL unsigned long long gcdbin(unsigned long long a,unsigned long long b)14 {15 if(!b) return a;16 if(!(a|0)&&!(b|0)) return 2*gcdbin(a>>1,b>>1);17 if(!(a|0)&&(b&1)) return gcdbin(a>>1,b);18 if((a&1)&&!(b|0)) return gcdbin(a,b>>1);19 return gcdbin(b,a%b);20 }21 unsigned long long a,b;22 int main()23 {24 freopen("rand_gcd.txt","r",stdin);25 cin>>a>>b;26 cout<
Code2

Algorithm3

不压位的高精度

高精度求余数很麻烦（按位求会比较快）

套用更相减损法

同时特判：如果a，b小于19位，依然采用二进制的辗转相除。

Code3

在GMOJ上……
Code3

由于是普通的更相减损，一旦数位超过20使用高精，速度就会很慢很慢很慢……

60分~80分不等

Algorithm4

高精压位

核心算法与Algorithm3相同

Code4

#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           #include
            
             #include
             
              #include
              
               #define IL inlineusing namespace std;const int L=1001;int a[L],b[L],t[L];int times=1;string stra,strb;bool fail;IL bool cmp(){ for(int i=L-1;i>=0;i--) { if(a[i]>b[i]) return 0; if(a[i]
               
                =0;i--) { if(a[i]&1) a[i-1]+=5; a[i]>>=1; }}IL void divb(){ for(int i=L-1;i>=0;i--) { if(b[i]&1) b[i-1]+=5; b[i]>>=1; }}IL void div2(){ diva(); divb();}int main(){// freopen("gcd.in","r",stdin);// freopen("gcd.out","w",srdout); cin>>stra>>strb; for(unsigned int i=0;i
                
                 >1)+(a[i]>>3); a[i]%=10; } else for(int i=0;i
                 
                  >1)+(b[i]>>3); b[i]%=10; } if(zeroa) for(int i=L-1;i>=0;i--) { if(a[i]) flag=1; if(flag) cout<
                  
                   =0;i--) { if(b[i]) flag=1; if(flag) cout<
Code4

Algorithm5

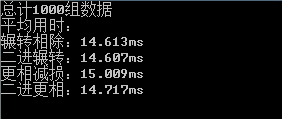
通过下面（最下面）的对拍发现，四种算法中，二进更相比普通更相更快（不是只有0.3毫秒么？）

高精（可以不压位）二进制更相减损术也不是很难打（而且判断也很快）

 

 

 

 

 

Impression

 如果你有兴趣……

#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           #include
            
             #include
             
              #include
              
               #define IL inlineusing namespace std;unsigned long long gcd(unsigned long long a,unsigned long long b){ return b==0?a:gcd(b,a%b);}unsigned long long a,b;int main(){ freopen("rand_gcd.txt","r",stdin); cin>>a>>b; cout<
gcd.cpp 
#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           #include
            
             #include
             
              #include
              
               #define IL inlineusing namespace std;unsigned long long gx(unsigned long long a,unsigned long long b){ if(a
               
                >a>>b; cout<
gx.cpp 
#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           
            #include
            #include
             
              #include
              
               #include
               
                #define IL inlineusing namespace std;IL unsigned long long gcdbin(unsigned long long a,unsigned long long b){ if(!b) return a; if(!(a|0)&&!(b|0)) return 2*gcdbin(a>>1,b>>1); if(!(a|0)&&(b&1)) return gcdbin(a>>1,b); if((a&1)&&!(b|0)) return gcdbin(a,b>>1); return gcdbin(b,a%b);}unsigned long long a,b;int main(){ freopen("rand_gcd.txt","r",stdin); cin>>a>>b; cout<
gcdbin 
#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           
            #include
            #include
             
              #include
              
               #include
               
                #define IL inlineusing namespace std;IL unsigned long long gxbin(unsigned long long a,unsigned long long b){ if(!b) return a; if(!(a|0)&&!(b|0)) return 2*gxbin(a>>1,b>>1); if(!(a|0)&&(b&1)) return gxbin(a>>1,b); if((a&1)&&!(b|0)) return gxbin(a,b>>1); if(a
                
                 >a>>b; cout<
gxbin.cpp 
#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           #include
            
             #include
             
              #include
              
               #include
               
                #include
                
                 #define IL inlineusing namespace std;int main(){ freopen("rand_gcd.txt","w",stdout); srand(time(NULL)); cout<<(unsigned long long)rand()*rand()*rand()<
rand_gcd.cpp 
#pragma GCC optimize(2)#include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #include
           #include
            
             #include
             
              #include
              
               #include
               
                #define IL inlineusing namespace std;int avg[4];int times;int main(){ system("random_gcd.exe"); int s1=clock(); system("gcd.exe"); int s2=clock(); system("gcdbin.exe"); int s3=clock(); system("gx.exe"); int s4=clock(); system("gxbin.exe"); int e=clock();// cout<<"\n辗转相除："<
                
                 <<"ms\n";// cout<<"二进辗转："<
                 
                  <<"ms\n";// cout<<"更相减损："<
                  
                   <<"ms\n"; // cout<<"二进更相："<
                   
                    <<"ms\n"; avg[0]+=s2-s1; avg[1]+=s3-s2; avg[2]+=s4-s3; avg[3]+=e-s4; times++; if(times>=100) { system("cls"); cout<<"总计"<
                    
                     <<"组数据\n"; cout<<"平均用时：\n"; cout<<"辗转相除："<
gcd对拍.cpp

1000组数据运算结果如下

End

转载于:https://www.cnblogs.com/send-off-a-friend/p/11389683.html

你可能感兴趣的文章
ArcGIS Server Javascript 多图对比功能
查看>>
微信上传素材返回 '{"errcode":41005,"errmsg":"media data missing"}'，php5.6返回
查看>>
div或者p标签单行和多行超出显示省略号
查看>>
Elasticsearch 滚动重启 必读
查看>>
Hadoop基本概念
查看>>
java.util.zip压缩打包文件总结一：压缩文件及文件下面的文件夹
查看>>
浅说 apache setenvif_module模块
查看>>
MySQL--数据插入
查看>>
重新学习python系列(二)？ WTF？
查看>>
shell脚本统计文件中单词的个数
查看>>
SPCE061A学习笔记
查看>>
sql 函数
查看>>
hdu 2807 The Shortest Path 矩阵
查看>>
熟悉项目需求，要知道产品增删修改了哪些内容，才会更快更准确的在该项目入手。...
查看>>
JavaScript 变量
查看>>
java实用类
查看>>
smarty模板自定义变量
查看>>
研究称90%的癌症由非健康生活习惯导致
查看>>
命令行启动Win7系统操作部分功能
查看>>
排序sort (一)
查看>>
喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！-- 愿君每日到此一游！
当前时间: 2024-11-25 20:21:52   当前IP: 3.12.123.41   联系邮箱:javaeecc@qq.com     Copyright © 2020 - 2022 baihongyu.com 京ICP备2021015314号-2
强烈建议你试试无所不能的CHAT-GPT，快点击我
强烈建议你试试无所不能的CHAT-GPT，快点击我